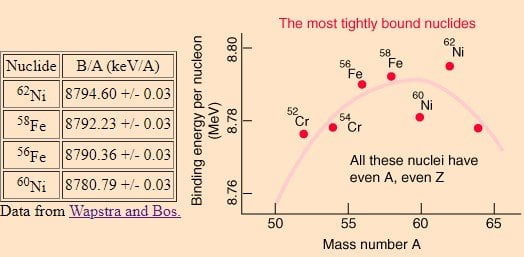
Which is the most stable nuclide? The popular verdict says $^{56} _{26}Fe$ is the most stable nuclide since it has the highest binding energy per nucleon $(\frac{B}{A}=8.790 \ MeV/A)$. However, this is incorrect. The most stable of all the nuclides is $^{62} _{28}Ni$. Its binding energy per nucleon is $(\frac{B}{A}=8.794 \ MeV/A)$. This post discusses why this incorrect information has prevailed for so long even in respectable academic spheres.
How is nuclear stability estimated?
The stability of a nucleus is measured along the same principle of physics that is applied elsewhere; the lesser the energy of a system, the more stable it is. That is, for a system to be stable, has to release some energy during its formation from its constituents. Conversely, this much amount of energy must be supplied to the stable system to destabilize and break it. In the case of a nucleus, it is taken as a system that consists of protons and neutrons. Neither a proton nor a neutron is an elementary particle. A neutron or a proton is considered a hadron, a composite particle made up of two or more quarks. These quarks interact with the neighbouring quarks through nuclear forces (weak and strong). These forces are responsible for the energy of a nucleus. By default, a quark is a matter particle that has a nonzero rest mass. Thus it has some rest mass energy in accordance with the mass-energy equivalence equation: $E_0=mc^2$. This energy, too, accounts for the energy of the nucleus it is a part of. The stability of the nucleus is measured by a parameter called the binding energy.
The Binding Energy of a Nucleus
A stable nucleus has less energy than the sum of the energies of its individual constituents. This difference is called the binding energy. If a nucleus has a mass M that is made up of $x$ protons (each of mass $m_p$) and $y$ neutrons (each of mass $m_n$), then, for the nucleus to be stable, the following condition must be satisfied. $$M<xm_p+ym_n$$
This tiny difference in mass, $\delta m$ is equivalent to a humongous amount of energy $E= \delta m c^2$. This is the nucleus’s binding energy, which is released when the nucleus is formed out of the constituent particles. On a statistical basis, nuclear physicists also define another parameter, binding energy per nucleon for stability estimates.
Binding Energy per Nucleon
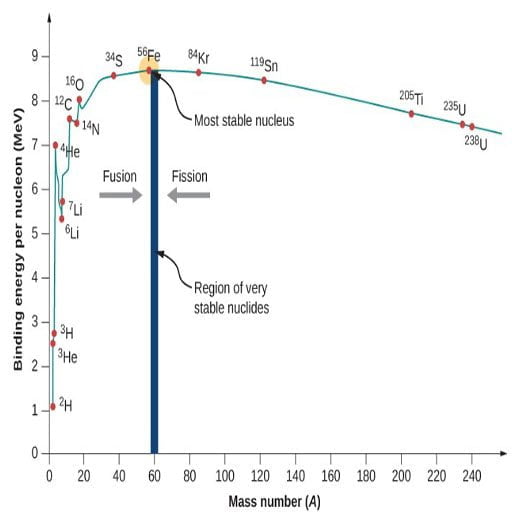
Each proton or neutron inside a nucleus is considered as a nucleon. The total number of protons in a nucleus is denoted by $Z$. The total number of neutrons is denoted by $N$. Thus the total number of nucleons is denoted by $A=Z+N$. If the nucleus has a binding energy $B$, the binding energy per nucleon is given by $\frac{B}{A}$, expressed in electronvolts per $A$. The following scatter plot shows the variation of $\frac{B}{A}$ with respect to $A$ for various elements of the periodic table.
Credit: BCcampus Open Publishing
The binding energy per nucleon on a nuclide also shows how tightly bound a nucleus is. The higher the binding energy the tighter it is, thus the more stable and harder to break it apart. Binding energy per nucleon is also called “average binding energy ($\overline{B}$)”.
How is the most stable nuclide identified?
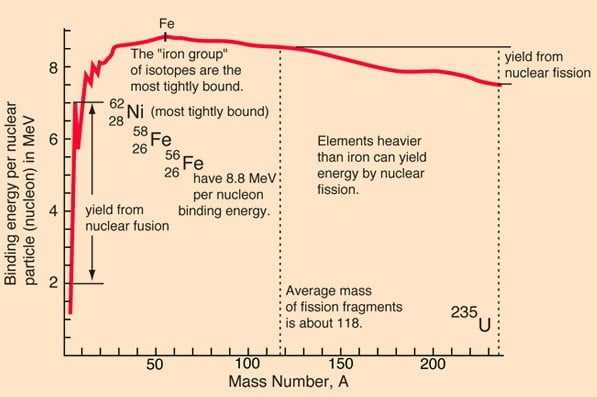
The B/A vs A curve may look smooth and continuous, it is actually a scatter plot. The mass numbers are distinct. The fluctuations in the value of B/A around the central tendency is partly due to the shell effect. Yet, a lot can be inferred just by studying the central tendency curve which appears to be continuous. The curve appears to be smooth for $A \geq 40$. It attains a maximum around $A=60$ and then begins to fall smoothly for heavier elements. Thus, a reasonable identification of the most stable nuclide can be done by precisely locating the maximum. It may sound easy but it’s very hard and ambiguous to pinpoint this maximum. Through repeated experiments done using the mass spectrometers of various precisions, it has been confirmed that the iron group (chromium-Cr, manganese-Mn, Iron-Fe, Cobalt-Co, and nickel-Ni) is the most stable group of all elements. However, due to the narrow margin between $^{56} _{26} Fe$, $^{58} _{26} Fe$, $^{60} _{28} Ni$, and $^{62} _{28} Ni$, it had been very hard to attribute the maximum to any one of these based on the statistical data. This is where the astrophysical data was used to reach a verdict.
Stellar Nucleosynthesis
Stellar nucleosynthesis is the process of the formation of heavier nuclei from lighter ones. Heavier nuclei require higher temperatures to be synthesized in the stellar cores. Starting from the fusion of helium-$^4 _2He$ from hydrogen-$^1 _1 H$, the process is exothermic. Thus, a sustainable nuclear chain reaction giving rise to heavier nuclei is feasible but only till the mass number A is near or below 60. Above A=60, nucleosynthesis becomes endothermic and cannot sustain as a chain reaction. Nuclides with A>>60 are formed only when stars collapse and produce shock waves that force smaller nuclides to combine. A thorough study of the end products of the sustained chain reactions in stellar nucleosynthesis has time and again confirmed that $^{56} _{26} Fe$ is the most abundant one of all. Thus, it was taken to be the most stable nuclide in conjunction with the binding energy data. However, with an increase in the sophistication of measurement of A with high-resolution mass spectrometers, this conclusion has been proven to be incorrect.
In his 1995 paper published in the American Journal of Physics, physicist M P Fewell has clearly settled the confusion. He has shown various reasons for the ambiguity that had prevailed earlier and has put forth his thorough justifications to conclude $^{62} _{28} Ni$ as the most stable nucleus of all. Below are a few of his reasonings.
The Processes in Stellar Nucleosynthesis
There are three processes in stellar nucleosynthesis: charged particle capture and photodisintegration. In a charged particle capture, an existing nucleus captures particles such as alpha ($^4 _2 He^{++}$), muon ($\mu ^-$) and electron ($e^-$), etc. and transforms into heavier nuclide. In a photodisintegration process, an existing nucleus captures a highly energetic photon and disintegrates into a lighter nuclide. Although both the processes require very high temperatures, photon capture tends to occur more frequently than the charged particle captures because charged particles encounter Coulomb forces in addition to the nuclear forces. That’s why sustained chain reactions in stellar nucleosynthesis end up with an abundance of $^{56} _{26} Fe$, where the equilibrium between both the processes is established. However, when estimated independent of the stellar nucleosynthesis, it is $^{62} _{28} Ni$ wins over $^{56} _{26} Fe$ albeit by a very narrow margin. Since the margin is less than 0.05%, it has been ignored over time.
Conclusion
A revised and improved investigation of the data yields the conclusive answer that indeed it is $^{62} _{28} Ni$ that should be considered as the most stable nucleus of all.